ANOVA

El análisis de la varianza (Anova) se debe al estadístico-genético Sir Ronald Aylmer Fisher (1890-1962),autor del libro "Statistics Methods for Research Workers" publicado en 1925 y pionero de la aplicación de métodos estadísticos en el diseño de experimentos, introduciendo el concepto de aleatorización. El Anova se puede utilizar en las situaciones en las que nos interesa analizar una respuesta cuantitativa,llamada habitualmente variable dependiente, medida bajo ciertas condiciones experimentales identificadas por una o más variables categóricas (por ejemplo tratamiento, sexo), llamadas variables independientes. Cuando hay una sola variable que proporciona condiciones experimentales distintas, el análisis recibe el nombre de Anova de un factor.Entre las pruebas de comparación múltiples a posteriori, que se utilizan a continuación de las técnicas del Anova, se encuentra la prueba HSD de Tukey. John Tukey es, asimismo  conocido por introducir la transformación rápida de Fourier, aunque trabajó en muchas áreas incluyendo sobre todo la filosofía de la estadística.Cuando el análisis de la varianza no es  aplicable debido a incumplimientos de las suposiciones del modelo,es necesario aplicar la prueba de Kruskal-Wallis para el contraste de k medianas. Esta prueba es una ampliación de la prueba de Mann-Whitney-Wilcoxon para dos medianas.La prueba de Kruskal-Wallis fue propuesta por William Henry Kruskal (1919- ) y W. Allen Wallis (1912-1998) en el artículo "Use of ranks in one-criterion variance analysis" publicado en el “Journal of American Statistics Association” en 1952.

SPSS: ANOVA de un Factor

El análisis de varianza (ANOVA) de un factor nos sirve para comparar varios grupos en una variable cuantitativa. Esta prueba es una generalización del contraste de igualdad de medias para dos muestras independientes. Se aplica para contrastar la igualdad de medias de tres o más poblacionesindependientes y con distribución normal. Supuestas k poblaciones independientes, las hipótesis del contraste son siguientes:

1. H0: μ1=μ2= …=μk Las medias poblacionales son iguales

2. H1: Al menos dos medias poblacionales son distintas

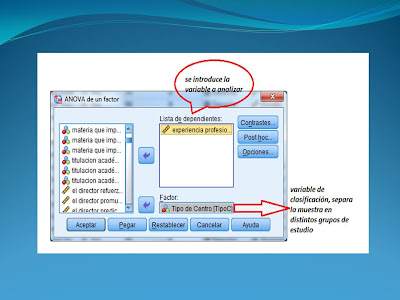
Para realizar el contraste ANOVA, se requieren k muestras independientes de la variable de interés. Una variable de agrupación denominada Factor y clasifica las observaciones de la variable en las distintas muestras.

Suponiendo que la hipótesis nula es cierta, el estadístico utilizado en el análisis de varianza sigue una distribución F de Fisher-Snedecor con k-1 y n-k grados de libertad, siendo k el número de muestras y n el número total de observaciones que participan en el estudio.

Para llevar a cabo un ANOVA de un factor:
Seleccionamos la opción:  Menú:
Analizar:
Comparar medias: ANOVA de un factor.

Al seleccionar el menú aparece el siguiente cuadro de diálogo:Si hacemos

Si hacemos clic en Opciones, aparece el cuadro de diálogo:

Aquí podemos solicitar los estadísticos que nos interesan para el contraste y marcar la opción para los valores perdidos.Marcamos Descriptivos y Homogeneidad de varianzas (el estadístico F del ANOVA de un factor se basa en el cumplimiento de 2 supuestos fundamentales: normalidad y homocedasticidad).


Utilizamos los contrastes llamados comparaciones múltiples post-hoc o a posteriori para saber qué media difiere de qué otra. Esas comparacionespermiten controlar la tasa de error al efectuar varios contrastes utilizando las mismas medias.Si hacemos clic en Post hoc aparece el cuadro

El cuadro de post hoc muestra las distintas pruebas post hoc para hacer comparaciones múltiples por parejas o pruebas de rango. Si la conclusión del contraste es rechazar la igualdad de medias se puede plantear qué grupos dos a dos son los que tienen medias significativamente distintas. Una forma de hacerlo sería plantear contrastes de igualdad de medias para dos muestras independientes con la prueba T de Student. Otra forma es utilizar una de las pruebas Post hoc que ofrece el análisis de la varianza. En particular, la prueba de Scheffé realiza todos los contrastes de igualdad de medias dos a dos y constituye dos distintos grupos homogéneos a partir de los resultados de los contrastes por parejas. Algunos autores destacan la prueba de Scheffé como más conservadora, así como la más utilizada, a pesar de que en muchas áreas se está imponiendo la de Bonferroni (Lizasoain y Joaristi; 2003: 363).

La tabla que contiene el estadístico de Levene nos permite contrastar la hipótesis de igualdad de varianzas poblacionales. Si el nivel crítico (sig.) es menor o igual que 0,05, debemos rechazar la hipótesis de igualdad de varianzas. Si es mayor , aceptamos la hipótesis de  igualdad de varianzas.

Prueba de homogeneidad de varianzas

Estadístico de  Levene	gl1	gl2 Sig.	gl2 Sig.
.929	3 64 .432	3 64 .432	3 64 .432

El siguiente paso nos lleva a la tabla de ANOVA, que nos ofrece el estadístico F con su nivel de significación. Si el nivel de significación (sig.) intraclase es menor o igual que 0,05, rechazamos la hipótesis de igualdad de medias, si es mayor – aceptamos la igualdad de medias, es decir, no existen diferencias significativas entre los grupos.

	Suma de cuadrados	gl	Media cuadrática	F	Sig.
Inter-grupos Intra-grupos Total	.482 30.518 31.000	3 67 64	.161 .477	.337	.798

Desde la tabla de comparaciones post-hoc vemos posibles combinaciones dos a dos entre los niveles de la variable factor (Variable 2), las diferencias entre las categorías de la variable 1 en cada grupo, el error típico de diferencias y nivel crítico asociado a cada diferencia (significación). Los grupos cuyas medias difieren de forma significativa (a nivel de 0,05) son los que presentan diferencias estadísticamente significativas entre sí.Cuando la F de la tabla de análisis de la varianza es no significativa, la conclusión es que el factor no influye en la variable dependiente, es decir, los distintos niveles del factor se comportan de igual forma en lo que a la variable dependiente se refiere.Pero si tal F es significativa sólo se puede concluir que, por lo menos, dos niveles del factor producen distintos efectos en al dependiente. Quiere esto decir que habrá que estudiar entre qué niveles se den esas diferencias significativas